Vortex Core Extraction Method

Problem:

How is the Vortex Core calculated in Tecplot 360?

Solution:

The exact Vortex Core extraction method is defined in an AIAA paper called “Identification of Swirling Flow in 3-D Vector Fields” by David Sujudi and Robert Haimes of the Massachusettes Institute of Technology.

Abstract
An algorithm for identifying the center of swirling flow in 3-D discretized vector fields has been developed. The algorithm is based on critical point theory and has been implemented as a visualization tool within pV3, a package for visualizing 3-D transient data. The scheme works with gridding supported by pV3: structured meshes as well as unstructured grids composed of tetrahedra, polytetrahedral strips, hexahedra, pyramids, and/or prism cells. The results have been validated using artificially-generated vector fields and 3-D CFD data.

Theory

1. Linearly interpolate the velocity within the cell.
2. Compute the rate-of-deformation tensor A. Since a linear interpolation of the velocity within the cell can be written as
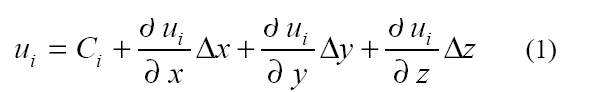
   then A can be constructed from the coefficients of the linear interpolation function of the velocity vector.
3. Find the eigenvalues of A. Processing continues only if A has one real (λR) and a pair of complex conjugate eigenvalues (λC).
4. At each node of the tetrahedron, subtract the velocity component in the direction of the eigenvector corresponding to λR. This is equivalent to projecting the velocity onto the plane normal to the eigenvector belonging to λR, and can be expressed as
   
   where n is the normalized eigenvector corresponding to λR, and w is the reduced velocity.
5. Linearly interpolate each component of the reduced velocity to obtain
   
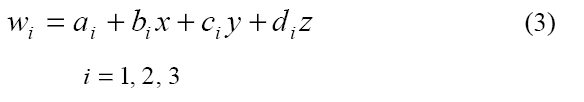
6. To find the center, we set wi in equation 3 to zero. Since the reduced velocity lies in a plane, it has only 2 degrees of freedom. Thus, only 2 of the 3 equations in equation 3 are independent. Any 2 can be chosen as long as their coefficients are not all zero. Now we have
   
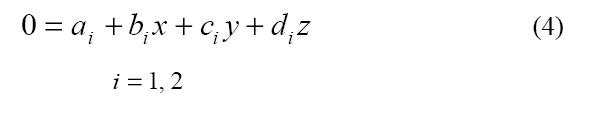
7. If this line intersects the cell at more than 1 point, then the cell contains a center of a local swirling flow. The center is defined by the line segment formed by the 2 intersection points.