< Back

Calculating the Volume of an Iso-Surface

Calculation, Derived Objects, Tecplot 360, Vector June 28, 2019

Question:

How do I calculate the volume of a completely enclosed iso-surface?

Solution:

The volume of an iso-surface (no holes in it) may be calculated using 360’s data calculation, alteration and integration features by following these steps:

A)   First, create a zone from your iso-surface:

  1. Display the iso-surface of choice by going to the side panel and clicking the Iso-Surfaces Details… button.
  2. Activate only one iso-surface group and ensure that it has no holes. See Figure 1.
  3. Select Data/Extract/Iso-Surfaces, click Extract, then OK.

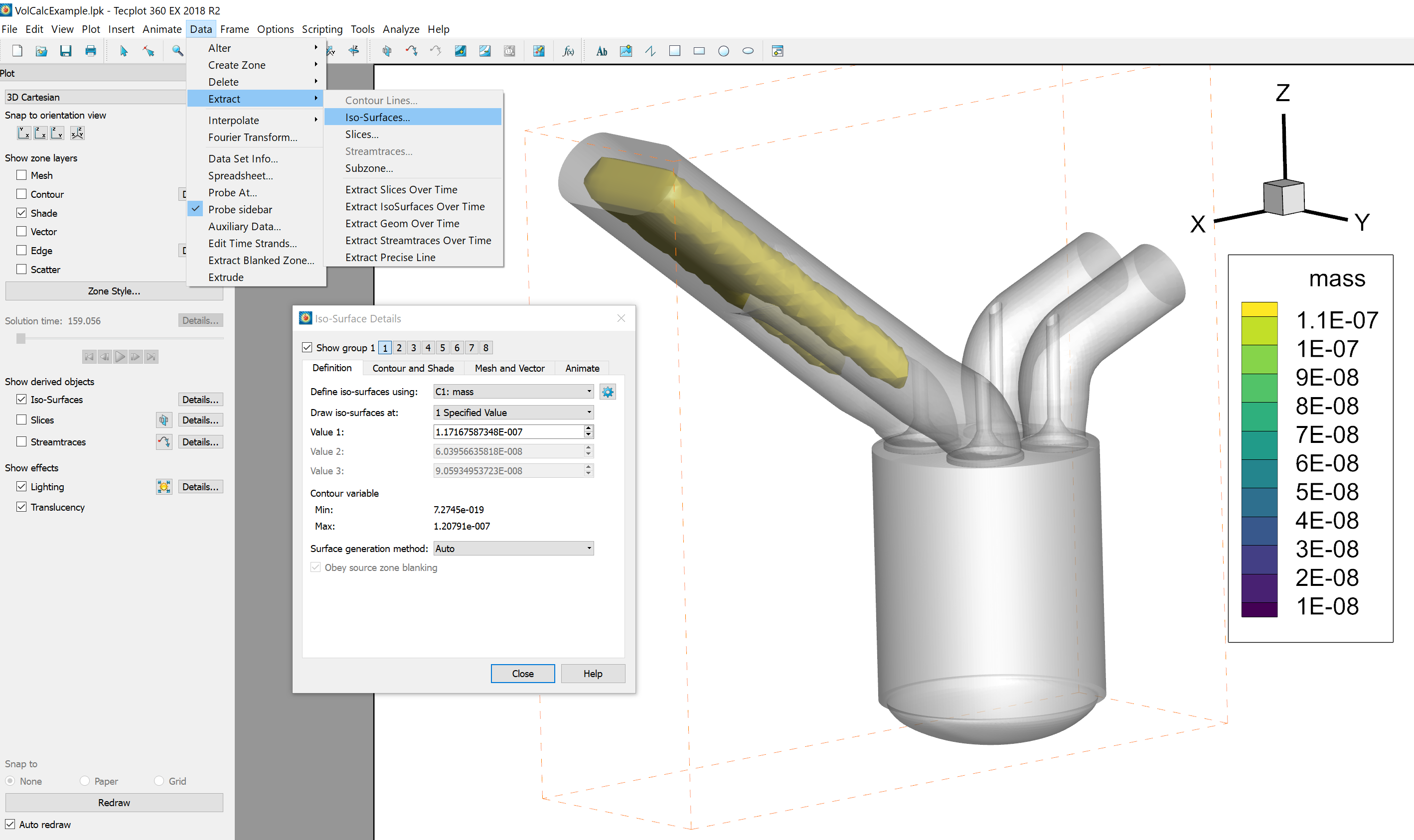
Figure 1: Extracting the iso-surface

 

B)  Next, calculate the surface unit normal:

  1. Select Analyze/Calculate Variables…
  2. Click on Select and choose Grid K Unit Normal (vector).
  3. For New Var Location, select Cell center. Make sure Calculate on Demand  is deactivated.
  4. Click Calculate, then Close.

C)   [Optional] Display the surface unit normals:

  1. Select Plot/Vector/Variables…
  2. For the vector components, select X Grid K Unit Normal, Y Grid K Unit Normal, and Z Grid K Unit Normal, and click OK.
  3. Turn on the Vector zone layer and observe the direction the vectors are pointing. If the vectors are pointing out of the surface, the calculated volume will be positive, otherwise it will be negative.

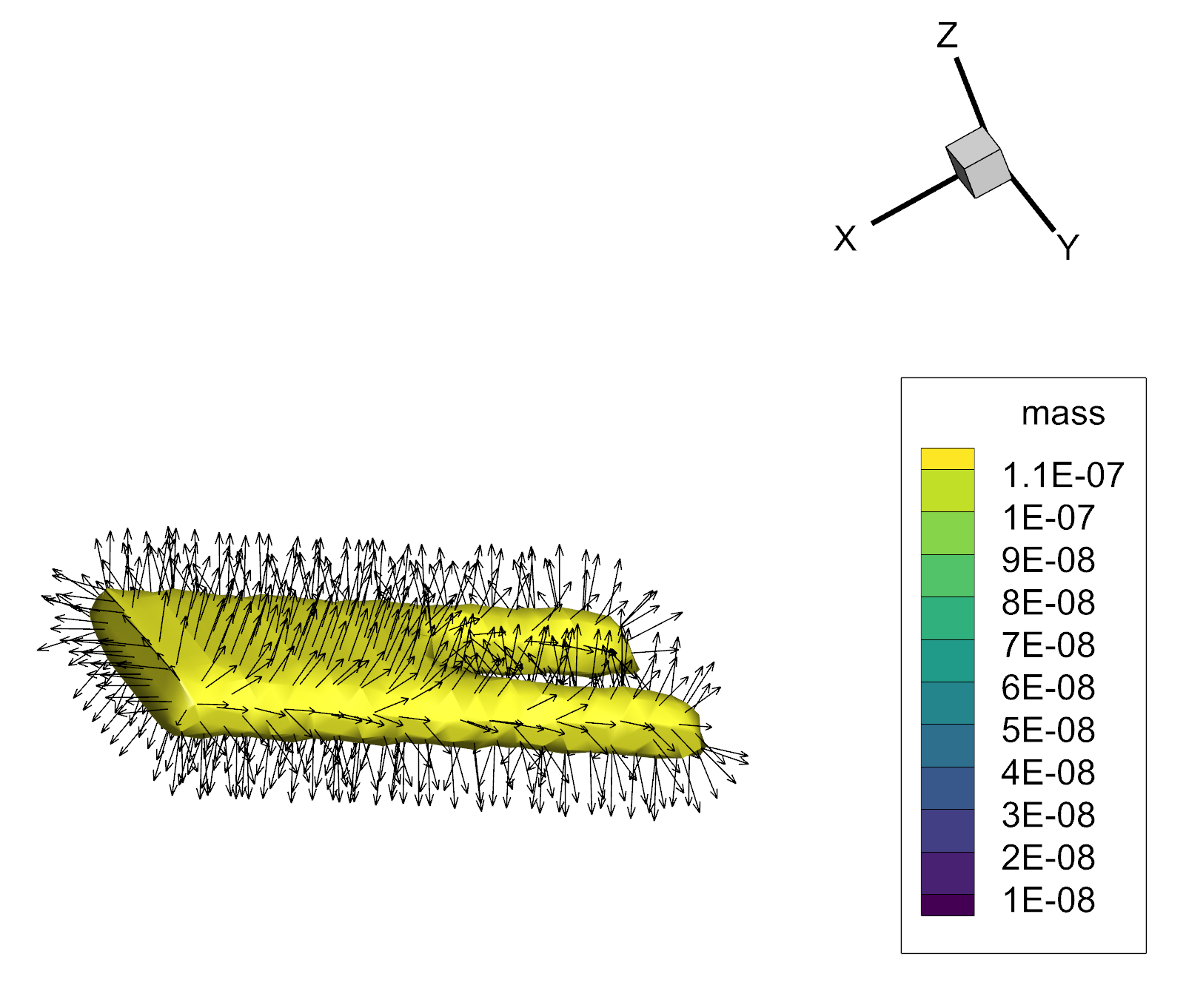
Figure 2: Displaying the calculated surface unit normals on the extracted iso-surface

 

D)   Then, calculate the scalar integrand:

  1. Select Data/Alter/Specify Equations.
  2. Enter the equation  {RdotN}=(X*{X Grid K Unit Normal} + Y * {Y Grid K Unit Normal} + Z * {Z Grid K Unit Normal}) / 3.
  3. For New var location, select Cell center. In Zones to Alter, select the extracted iso-surface zone entitled something like “Iso: C=1.17…” (see Figure 3).
  4. Click Compute, then OK, then Close.

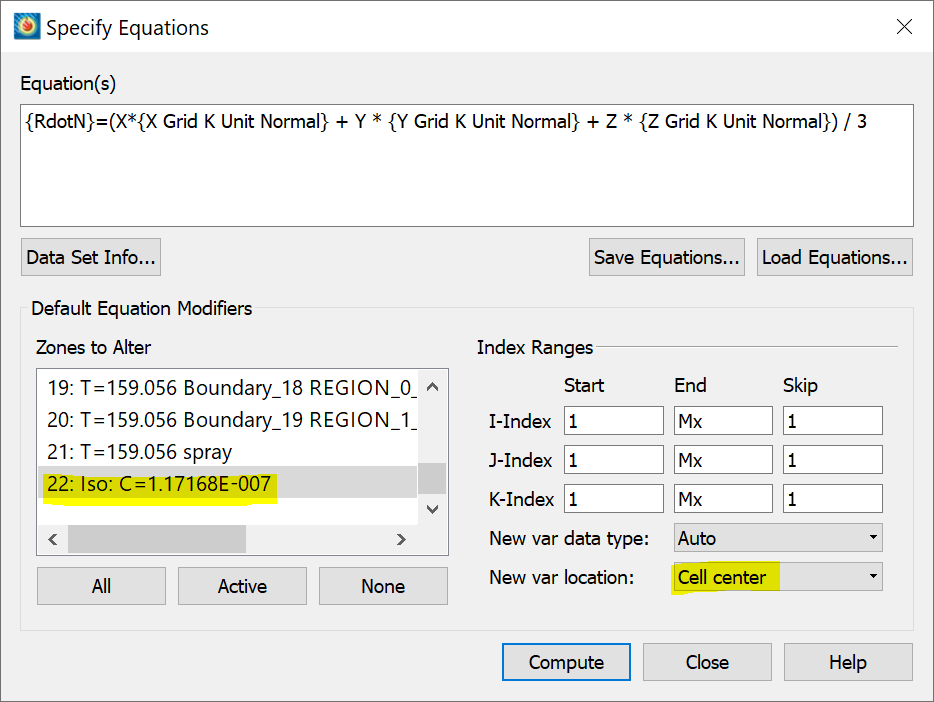
Figure 3: Calculating the scalar integrand

 

E)   Finally, integrate the scalar integrand to calculate the volume (see Figure 4):

  1. Select Analyze/Perform Integration…
  2. For Type of Integration, choose Scalar Integral.
  3. Click Select… to select the Scalar Variable, choose variable RdotN, and click OK.
  4. For Zones, enter the zone number of the extracted iso-surface. To find the zone you want, click Select….
  5. Activate Show Tabulated Results.
  6. Click Integrate. The volume is the integration total.

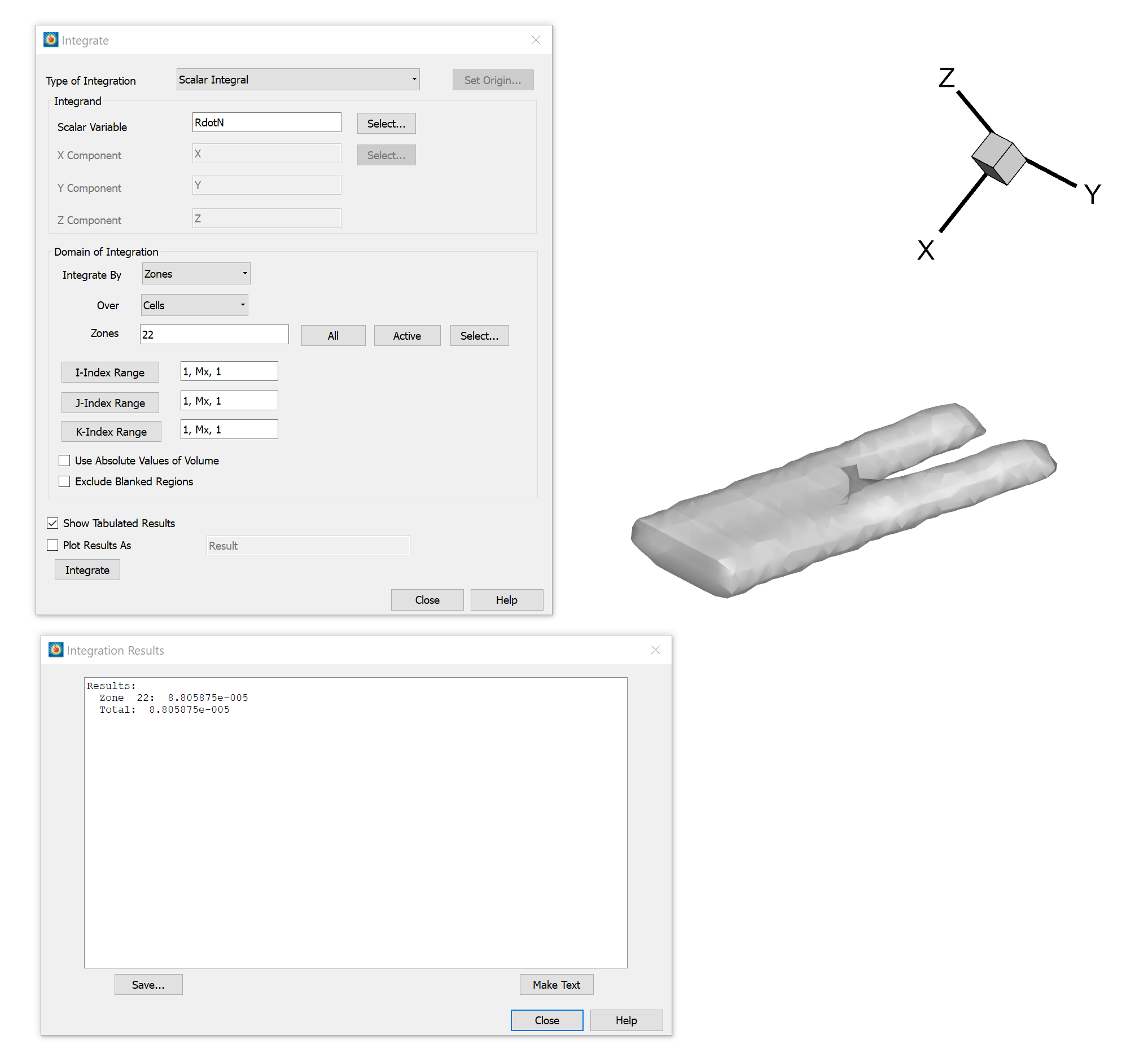
Figure 4: Integrating the scalar integrand and calculating the volume of the iso-surface

 

In this example, the total volume of the iso-surface is 8.81*10-5 cubic units.

Tecplot 360 Categories