< Back

Calculating Average Normal Velocity to Iso-Surface

Calculation, Tecplot 360, Vector April 16, 2019

Problem:

How do I calculate the average normal fluid velocity (or any vector variable) going through an iso-surface?

Details: Or stated another way, “I am trying to use a vector dot product with unit normal integration to get the average normal velocity through an extracted iso-surface.”  This question originally relates to this scenario, but it can be used for calculating the average flux though a surface for various cases.

Solution:

Tecplot 360 will approximate the following integrals:

1)  First, specify your iso-surface (see Iso-Surfaces Details… on the side panel), and then extract your iso-surface (Data –> Extract –> Iso-Surfaces…).

  • If you have transient data, make sure your iso-surface has a new time strand compared to the rest of your data. Make sure the iso-surface in other solution times are assigned to this time strand by going to Data –> Edit Time strands….

2)  Now it is time to calculate our integrals. Review the tips in “Performing Integrations” section of the User’s Manual and make sure you have the appropriate Fluid Properties…, Reference Values…, and Field Variables… as required. This example only requires the convection field variables to be set (e.g. Vel_U, Vel_V, and Vel_W). We will start by calculating the “Vector Dotted with Unit Normal,” as described in the User’s Manual. It is the integral of the numerator in the equation above:

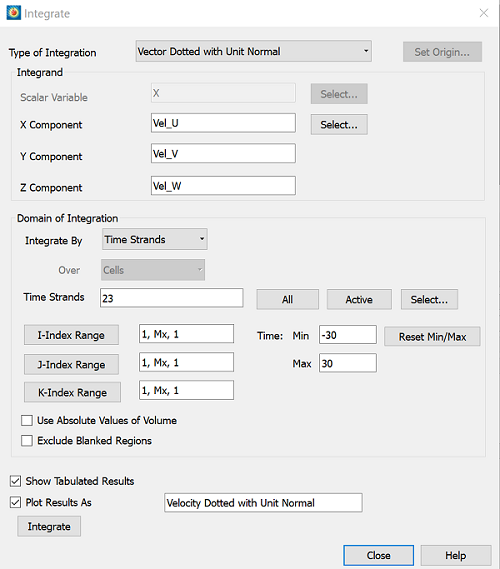
  • For calculating the velocity normal to the surface of the iso-surface, we will use the variable components of the velocity vector in our data set, in this case: Vel_U, Vel_V, and Vel_W. Integrate by the extracted iso-surface zone or time strand.
  • Note: The normal vectors are calculated within the integration function, but the direction of these normal vectors must be verified. You can view these vectors by following the procedure in the section “Surface Normal Calculations” in the User’s Manual.

3)  Calculate your second integral, the surface area of the iso-surface with the “Length/Area/Volume” integral. This is the integral in the denominator of the equation above.

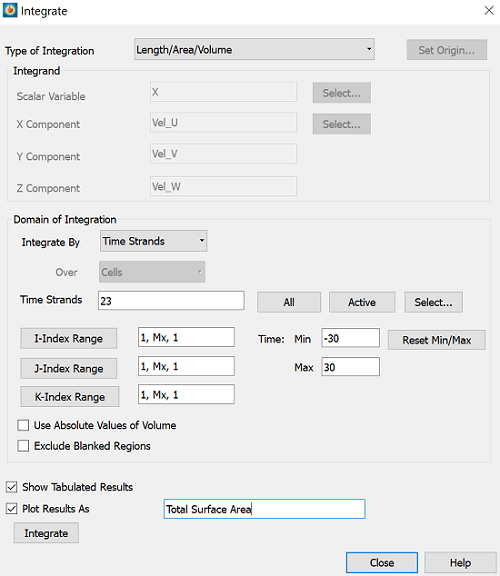
4)  Then, in order to find the average normal velocity to the iso-surface, manually calculate the following: Divide the “Vector Dotted with Unit Normal” integral from step 2 by the “Length/Area/Volume” integral calculated in step 3:

Average Velocity in Normal Direction Through Iso-Surface = (VectorDotNormal) / (Area)

This gives the average normal velocity going through the isosurface for a single zone (one time solution) or you can calculate it over a time strand.

Tecplot 360 Categories